Lecture 8 - Advanced parallel algorithms

Advanced recursive decomposition

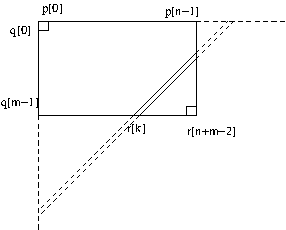
Sometimes, recursive decomposition can be done more efficiently in a way in which the parts are not straightforward, but reduce the number of operations.

Basic example of such decomposition: compute a complex product by using only 3 (instead of 4) real multiplications).

Solution: (a+bi)*(c+di) = (ac-bd) + (ad+bc)i = (ac-bd) + (ac+ad+bc+bd-ac-bd)i = (ac-bd) + ((a+b)*(c+d) - ac - bd)i, which can be computed using only 3 real multiplications (but more additions/substractions).

Polynomial multiplication using Karatsuba algorithm

Note: for the classical algorithm, computing the coefficients leads to computing the products and then add diagonals in the following table:

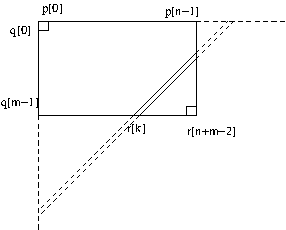
Idea:

• Split each of the input polynomials in half;
• Instead of multiplying each of the 4 pairs from the step above, use a similar trick to make only 3 multiplications

Assume input polynomials P(X) and Q(X) of degree 2*n-1.

Write them as P(X) = P₁(X)*X^n+P₂(X) and Q(X) = Q₁(X)*X^n+Q₂(X).

Now P(X)*Q(X) = (P₁(X)*X^n+P₂(X)) * (Q₁(X)*X^n+Q₂(X)) =
= P₁(X)* Q₁(X)*X^2n + (P₁(X)*Q₂(X)+P₂(X)*Q₁(X))*X^n + P₂(X)*Q₂(X)

But the second term can be written as
(P₁(X)+P₂(X)) * (Q₁(X)+Q₂(X)) - ₁(X)* Q₁(X) - P₂(X)*Q₂(X)