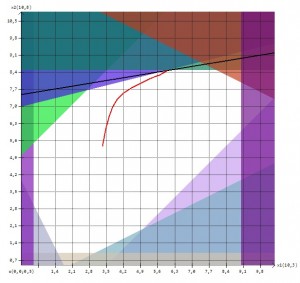
A centrális út (Az illusztráció az Antal Szabolcs-Csongor által írt Belsőpontos algoritmusok szemléltetése című szakdolgozat keretében készített alkalmazás segítségével készült.)

2013. április 17-én, az intézeti tudományos szeminárium keretében dr. Darvay Zsolt adjunktus előadására került sor Primál-duál belsőpontos algoritmusok keresési irányai címmel.

A lineáris és nemlineáris optimalizálás belsőpontos módszereinek körét az teszi változatossá, hogy egy kezdeti pontból kiindulva, különböző keresési irányokat választhatunk meg, és ez által az algoritmusoknak számos családja hozható létre. Az elmozdulási irányok megválasztásának két alapvető lehetőségéről volt szó. Az első eljárás a barrier-függvények használatán alapszik, amely az önkorlátozó és önreguláris függvényekkel van kapcsolatban. A második esetén előbb a centralizálási összefüggés ekvivalens algebrai átalakítását végezzük el, majd a Newton-módszert alkalmazzuk a keresési irányok meghatározásának érdekében.

Ez utóbbi technika előbb lineáris optimalizálásra volt bevezetve, de később az alábbi feladattípusokra általánosították: konvex kvadratikus optimalizálás, lineáris feltételektől függő konvex optimalizálás, lineáris komplementaritási feladat, szemidefinit programozás, konvex kvadratikus szemidefinit programozás, szemidefinit lineáris komplementaritási feladat, másodrendű kúpprogramozás, szimmetrikus optimalizálás és lineáris komplementaritási feladat szimmetrikus kúpokon.

Az előadás keretében említésre került az a tény is, hogy a belsőpontos módszerek különböző szempontok szerint osztályozhatóak. Beszélhetünk primál, duál, illetve primál-duál algoritmusokról. A megoldási eljárást tekintve affin skálázású, trajektóriakövető, illetve projektív potenciálfüggvényes algoritmusokat különböztetünk meg. A trajektóriakövetők osztályába sorolhatóak a centrális utat követő, a súlyozott, a nem megengedett, a prediktor-korrektor algoritmusok, egyes magasabb rendű, illetve altér módszerek. A lépéshossz szemszögéből nézve rövid, illetve hosszú lépéses algoritmusokat említhetünk meg.

Végül, az előadás a szemidefinit optimalizálásra, az euklideszi Jordan algebrákra és a szimmetrikus optimalizálásra vonatkozó alapvető kérdések bemutatásával zárult.